[Algorithm] 20. 문자열

KMP 알고리즘

어떤 긴 문자열 H에서 N=”aabaabac” 를 찾는 경우를 예를 들어보자.

시작 위치 i부터 N을 맞춰보니 첫 일곱 글자는 일치했지만 마지막 여덟 글자에서 불일치 했을 경우, 다음 위치인 i+1에서 다시 답을 찾기 시작한다.

일곱 글자가 대응되었다는 사실을 이용하면 시작 위치 중 일부는 답이 될 수 없을 보지 않아도 된다.

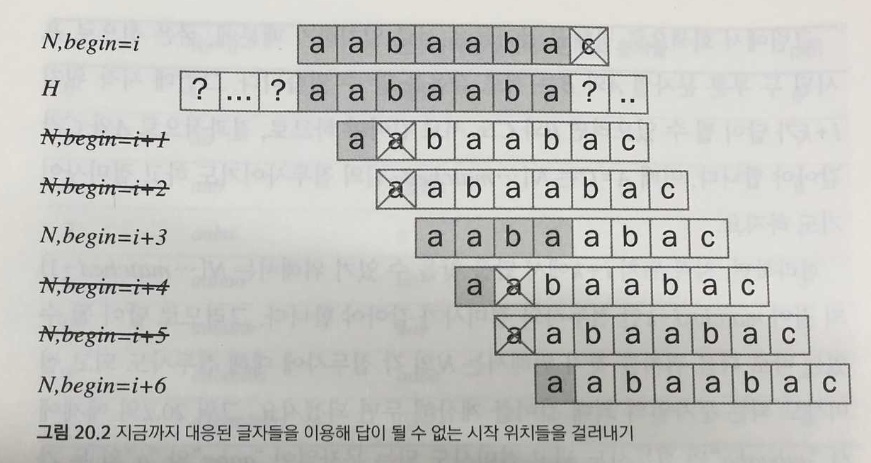
그림 20.2를 보면, 위치 i에서 일곱 글자가 일치하기 위해서는 H의 부분 문자열인 H[i..i+6]이 “aabaaba” 이어야 한다.

이 경우, i+1 에서 시작하는 N은 H와 일치할 수 없다.

H 문자열의 i+6까지 시작 위치를 하나씩 시도해보면 답이 될 가능성이 있는 시작 위치는 i+3과 i+6 밖에 없다.

시작 위치를 i+3으로 증가시키고 검색을 계속한다.

시작 위치 후보를 걸러낼 때 쓰는 정보는 현재 시작위치에서 H와 N을 비교했을 때 몇글자나 일치했는가를 사용한다.

다음 시작 위치 찾기

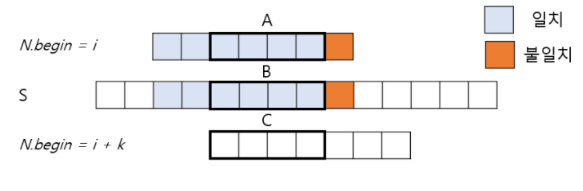
문자열 S에서 부분 문자열 N이 일치하는 S의 시작 위치 인덱스를 찾으려고 한다.

문자열 S의 i번째에서 N을 비교해보니, 마지막 부분이 불일치한다.

다음 시작 위치를 찾으려고 한다면, A,B,C 부분이 일치하니 이 일치하는 문자열의 시작 위치에서 다시 탐색을 시작한다.

시작 위치 i+k에서 답을 찾으려면, N[..matched-1]의 길이 matched-k인 접두사와 접미사가 같아야 한다.

그림 20.2의 예제에서 “aabaaba”의 접두사도 되고, 접미사도 되는 문자열이 “aaba”와 “a”의 두 가지가 있다.

“aaba”를 이용하여 시작 위치를 3만큼 옮겼다.

KMP 알고리즘은 전처리 과정에서 배열 pi[]를 계산하여 정의한다.

pi[i] = N[..i] 의 접두사도 되고 접미사도 되는 문자열의 최대 길이

pi[i]는 N이 어디까지 일치했는가를 주어질 때 다음 시작위치를 말해주기 때문에, 부분 일치 테이블(partial match table)이라고 한다.