[Algorithm] 18. 선형 자료 구조

동적 배열의 재할당 전략

재할당 코드조각에서 배열의 용량을 한 번에 M씩 늘렸다.

M번의 append() 연산 후에는 재할당이 일어난다는 의미와 같다.

예를 들어,

M=100 이라면, 재할당 마다 100개 여유분을 할당받는다.

처음 생성된빈 배열의 용량이 100이 된다.

append() 연산을 1만번을 수행한다면 다음과 같이 된다.

배열의 크기

100, 200, 300, … , 9900

append() 1만번 호출하면, 50만 번의 복사가 필요하다.

100+200+300+…9900 = 495,000

M을 늘리면 어떨까?

M=1000 이라면, 1만번의 append() 연산은 재할당을 아홉 번만 하면된다.

총 원소 복사의 수는 1000 + 2000 + … + 9000 = 45,000

하지만, 크기가 3인 정수 배열을 저장하는데도 1000개의 공간을 할당받아야하므로 낭비가 심하다.

재할당의 수 K = O(N/M)

M = 재할당시 배열을 늘리는 크기

N = append() 연산 횟수

전체 복사하는 원소의 수

M + 2M + … K*M =

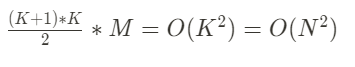
N 번의 append() 연산시 드는 시간이 O(N^2) 이다.

한번의 append() 연산은 O(N^2) / N = O(N) 이다.

여전히 상수시간이 아니다.

상수 시간에 append()를 구현하는 비결은?

• 재할당을 할 때마다, 정해진 개수의 여유분을 확보하는게 아니라.
• 현재 가진 원소의 개수에 비례해서 여유분을 확보해야 한다.

재할당 시점(size = capacity 일 때)	1	2	4	8	…	2048	4096	8192
새 배열의 크기	2	4	8	16	…	4096	8192	16384

8192번 째 append() 연산시 복사의 총 수는

1 + 2 + 4 + … + 8192 = 16383

i	0	1	2	…	i
복사하는 원소의 수	1	2	4	…	2^i