[Algorithm] 19. 큐와 스택, 데크
스택과 큐의 활용
예제: 스택을 이용한 울타리 자르기 문제의 해법
스위핑 알고리즘과 스택을 사용해서 O(N)시간에 동작한다.
💡 스위핑 알고리즘(sweeping algorithm) : 한 쪽 방향부터 시작해서 다른 방향으로 스캔해가면서 쓸어가는 방식으로,
이미 연산이 진행된 이전 공간에 대해서는 연산을 하지 않는다.
최대 사각형의 넓이
</br>
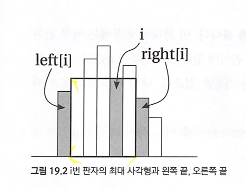
(right[i]-left[i]-1)*h[i]
- </br>
-
모든 판자에 대해 최대 사각형의 넓이를 구한 후, 그중 최대치를 구한다.
</br>
사각형의 넓이를 구하기 위해 필요한 것
- 왼쪽 끝
- 오른쪽 끝
- 높이
</br>
사각형의 특징
- 사각형의 높이는 i 번 판자와 항상 같다.
- 사각형의 왼쪽 끝과 오른쪽 끝은 i번 판자보다 낮은 판자들로 막혀있다.
- 즉, left[i] 와 right[i] 의 높이는 h[i] 보다 작다.
예)
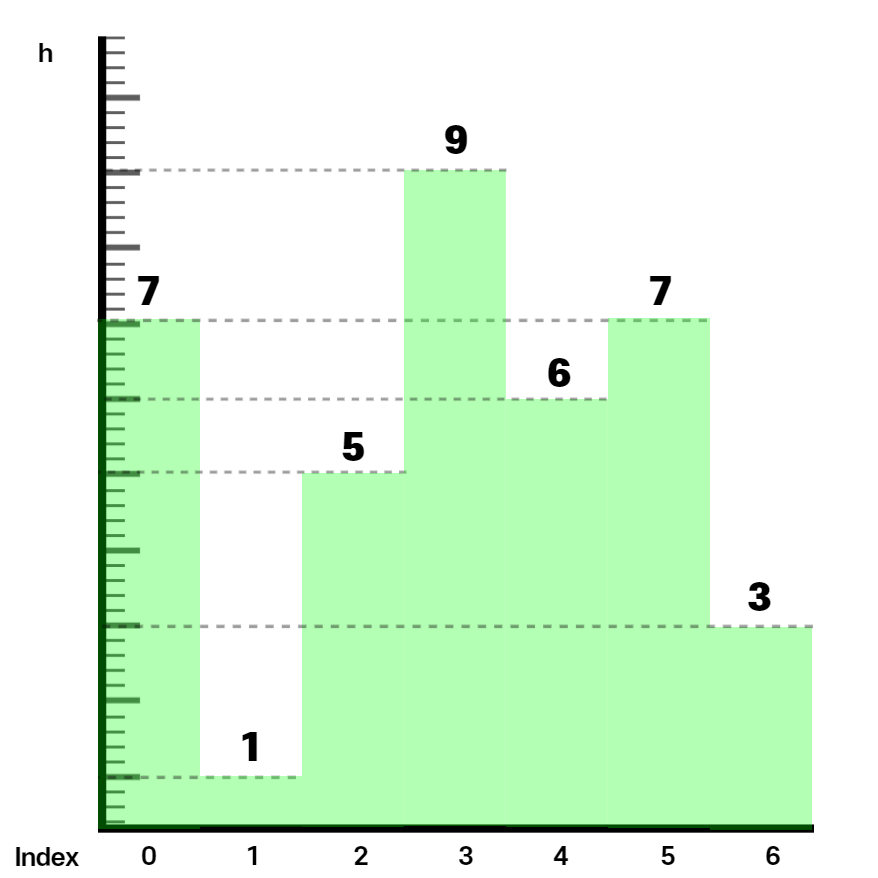
0번 판자의 왼쪽에 아무 판자도 없기 때문에 높이가 0인 판자가 -1 위치에 있다고 가정 : left[0] = -1
h[0] > h[1]
사각형의 왼쪽 끝과 오른쪽 끝은 i번 판자보다 낮은 판자들로 막혀있다. 앞서 정의된 사각형의 위 특징을 유의하여 사각형의 넓이를 계산해보면
왼쪽 끝 높이 : 0 0번 판자 높이 : 7 오른쪽 끝 높이 : 1 최대 사각형의 길이 막혀 0번 판자가 정의하는 최대 사각형을 찾을 수 있다.
따라서 여기서 최대 사각형의 넓이를 계산한다.
i = 0 일 때, left[0] = -1, right[0] = 1
// ( right[i] - left[i] - 1 ) * h[i]
(1 - (-1) -1 ) * 7 = 7
계산하고 나면 0번 판자는 의미가 없다. 왜? 0번 판자보다 1번 판자가 더 낮기 때문에, 이후의 어떤 판자 i 에 대해서도 left[i] = 0 이 될 일이 없다. 따라서 0번 판자를 지운다. 그러면 left[1] = -1 이 된다.
</br>
h[0] < h[1]
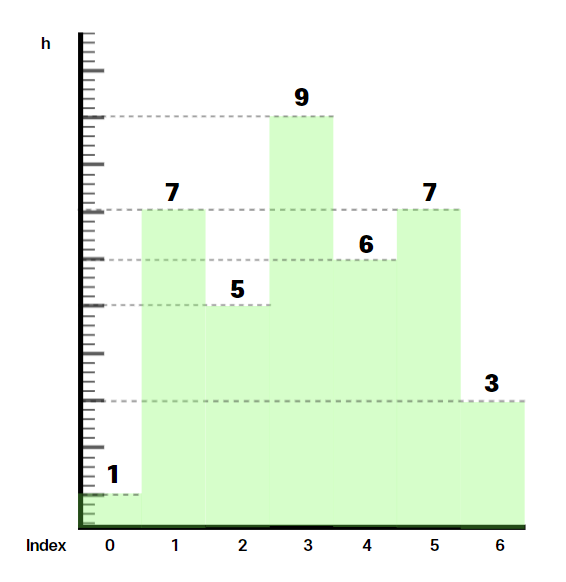
이 경우, 0번 판자가 1번 판자의 최대 사각형의 갈 길을 막고 있다. left[1] = 0
h[0] = h[1]
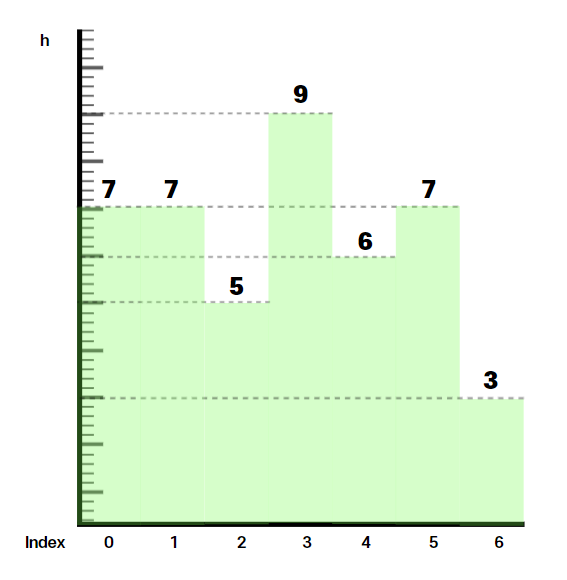
이 경우, 두 판자의 최대 사각형은 동일하다. 따라서 0번 판자를 남겨둘 이유가 없으므로 h[0] > h[1] 과 똑같이 처리한다. 두 판자의 최대 사각형이 동일한 이유 left[0] = -1, right[0] = 2 left[1] = -1, right[1] = 2 h[0] = h[1] = 7
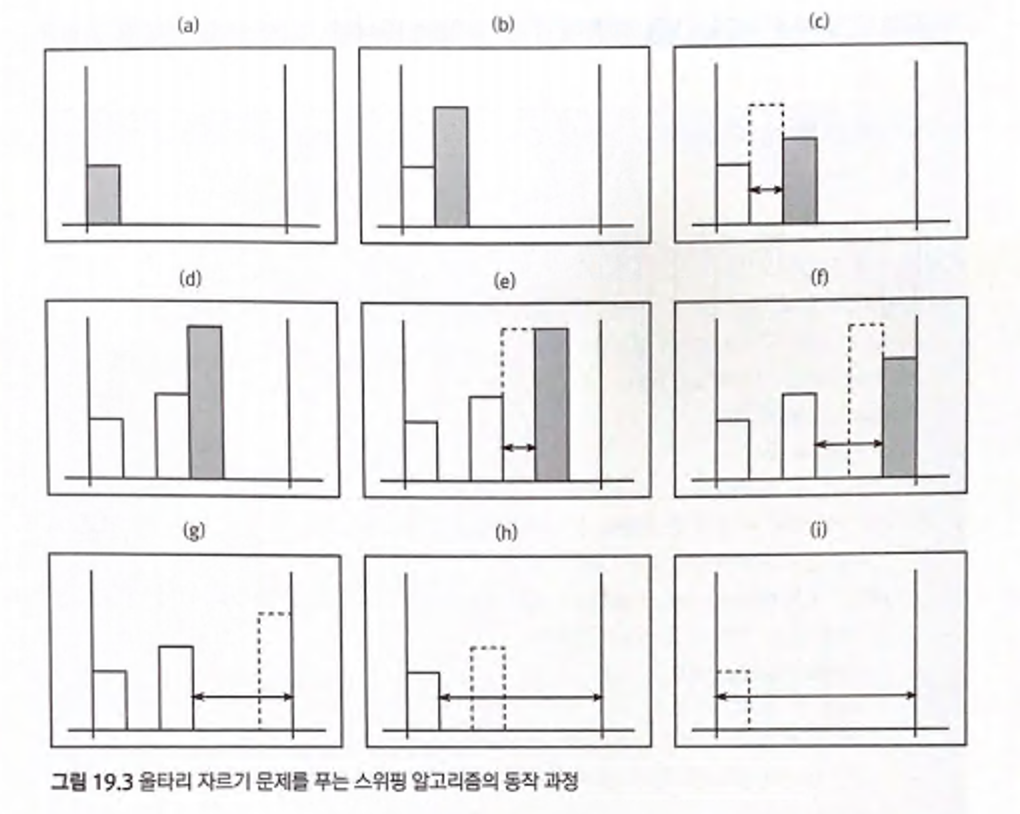
위 과정을 일반화하면 i 번 판자를 봤을 때 왼쪽에 자신보다 높은 판자들이 남아있다면 이들 전부에 대해 최대 사각형의 넓이를 계산하고 이들을 지운다. 그러면 i 번 판자 왼쪽에는 자신보다 낮은 판자만 남는다. 이로써 left[i] 를 알아낼 수 있다.
</br>
높이가 오른쪽 끝의 높이라고 했을 때, 왼쪽으로 연속된 판자들 중 이 높이를 포함하는 가장 낮은 지점이 왼쪽 끝이 된다. 따라서, 스택에 나중에 저장된 위치의 높이보다 현재 울타리 위치가 낮을 때, 그 전 사각형 영역을 계산한다.
</br>
아직 지워지지 않은 판자 (최대 사각형의 넓이가 계산 되지 않은 판자) 를 스택에 넣는다.
- 남아있는 판자 중 가장 오른쪽에 있는 (높이 0의 가상의) 판자와 i 번째 판자를 비교
- 판자를 제거할 때도 가장 오른쪽에 있는 판자를 제거