[Algorithm] 19. 큐와 스택, 데크

스택과 큐의 활용

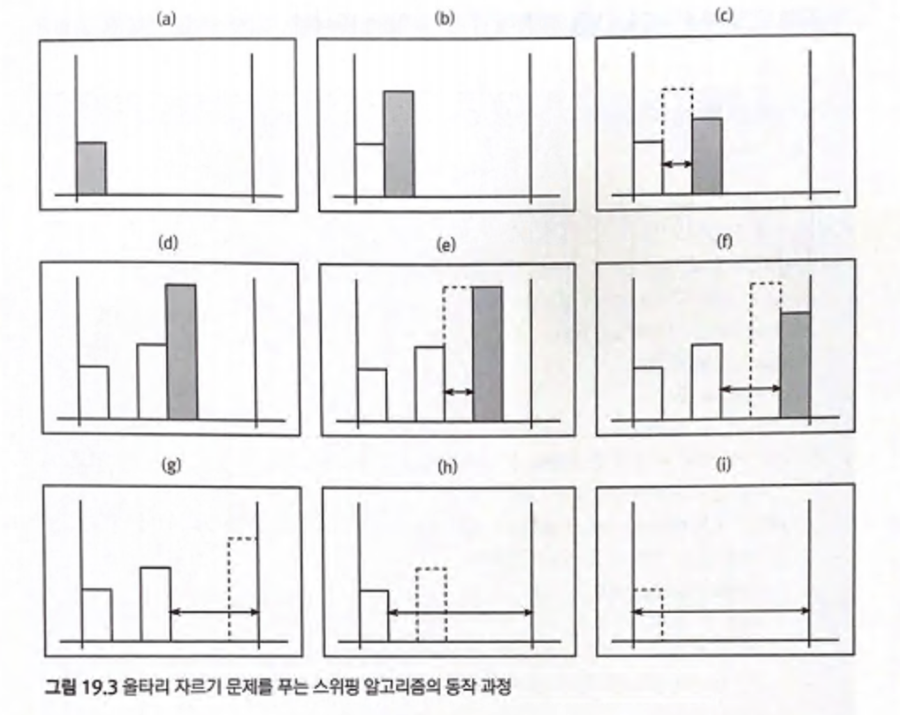
예제: 스택을 이용한 울타리 자르기 문제의 해법

구현

// 각 판자의 높이를 저장하는 배열
vector<int> h;

// 스택을 사용한 O(n) 해법
int solveStack() {
	// 남아있는 판자들의 위치들을 저장한다.
	stack<int> remaining;
	h.push_back(0);
	int ret = 0;
	for (int i = 0; i < h.size(); i++) {
		// 남아있는 판자들 중 오른쪽 끝 판자가 현재 높이 h[i] 보다 높다면
		// 이 판자의 최대 사각형은 i 에서 끝난다.
		while (!remaining.empty() && h[remaining.top()] >= h[i]) {
			int j = remaining.top();
			remaining.pop();
			int width = -1;
			// j 번째 판자 왼쪽에 판자가 하나도 안 남아 있는 경우 left[j] = -1
			// 아닌 경우 left[j] = 남아있는 판자 중 가장 오른쪽에 있는 판자의 번호가 된다.
			if (remaining.empty())
				width = i;
			else
				width = (i - remaining.top() - 1);
			ret = max(ret, h[j] * width);
		}
		remaining.push(i);
	}
	return ret;
}

1. 과정 이해하기

(stack 에 남은 가장 오른쪽인자 : stack R)

(a) remaining 에 쌓인 데이터가 없으니 stack 에 넣고 통과한다.

remaining.push(i);

(b) 현재 블록이 아직 stack R 보다 크므로 아직 최대 사각형 끝이 안나왔으므로 쌓아주고 넘어간다

remaining.push(i);

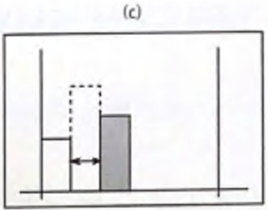
(c) 드디어 현재 블록이 stack R 보다 작다 == 최대 사각형의 마지막 포인트이므로 연산해준다.

//while 문 조건 성립
int j = remaining.top(); // stack R 꺼내서 저장하고
remaining.pop(); // 지우고

int width = -1;
//stack 에 값이 비어있으면 가장 왼쪽 포인트이므로 width = i
			if (remaining.empty())
				width = i;
//아니면 i = 2 이므로 2 - 0 - 1 = 1 이므로 너비 1
			else
				width = (i - remaining.top() - 1);

// 높이(2번째 판자 stack R 의 높이) x 너비(1)
ret = max(ret, h[j] * width);

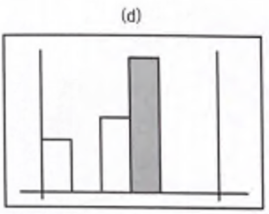
(d) 에서 현재 블록이 remaining 이 empty 상태가 아니고, 현재 높이가 stack R 보다 크니까 while 통과하고 스택에 쌓아주고 넘어간다

remaining.push(i);

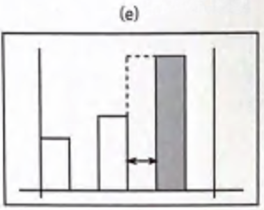
(e) 현재 블록이 stack R 과 같아도 조건으로 들어간다.

while (!remaining.empty() && h[remaining.top()] >= h[i]) {...

int j = remaining.top(); // stack R 꺼내고
remaining.pop(); // 지우고

int width = -1;
//stack 에 값이 비어있으면 가장 왼쪽 포인트이므로 width = i
			if (remaining.empty())
				width = i;
//아니면 i = 4 이므로 4 - 2 - 1 = 1 이므로 너비 1
			else
				width = (i - remaining.top() - 1);

// 높이(4번째 판자인 stack R 의 높이) x 너비(1)
ret = max(ret, h[j] * width);

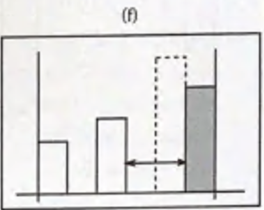
(f) stack R 보다 작은 값이 들어왔으므로 최대 사각형의 끝값이므로 (e) 와 같이 연산한다.

// stack R(5번째 판자) 꺼내서 j에 저장하고 지우고

// i = 5 이므로 5 - 2 - 1 = 2 이므로 너비 2
width = (i - remaining.top() - 1);

// 높이(5번째 판자인 stack R 의 높이) x 너비(2)
ret = max(ret, h[j] * width);

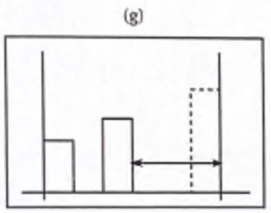
(g) for 문에 들어왔을 때 i = 6으로 값이 0 이므로 최대 사각형의 끝이다.

// stack R(6번째 판자) 꺼내서 j에 저장하고 지우고

// i = 6 이므로 6 - 2 - 1 = 3 이므로 너비 3
width = (i - remaining.top() - 1);

// 높이(6 번째 판자인 stack R 의 높이) x 너비(3)
ret = max(ret, h[j] * width);

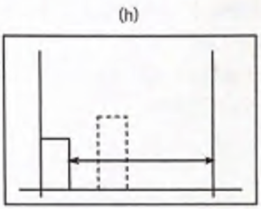
(h) 지웠는데도 stack R 이 현재 i = 6 의 높이(0)보다 크므로 2번째 while 문을 탄다.

// stack R (2번째 판자) 꺼내서 j에 저장하고 지우고

// i = 6 이므로 6 - 0 - 1 = 5 이므로 너비 5
width = (i - remaining.top() - 1);

// 높이(2 번째 판자인 stack R 의 높이) x 너비(5)
ret = max(ret, h[j] * width);

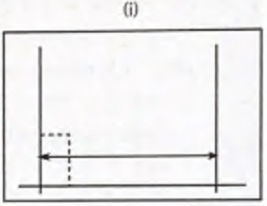
(i) 지웠는데도 stack R (첫번째 판자) 이 현재 높이(0)보다 크므로 3번째 while 문을 탄다.

// stack R (1번째 판자) 꺼내서 j에 저장하고 지우고

// remaining.empty 이므로 width = i = 6 
if (remaining.empty())
			width = i;

// 높이(1 번째 판자인 stack R 의 높이) x 너비(6)
ret = max(ret, h[j] * width);

이후에는 조건 중 !remaining.empty()로 인해 걸리지 않으므로 while 조건에서 넘어간다.

while (!remaining.empty() && h[remaining.top()] >= h[i]) {...

다음 for 문으로 넘어가고 i = 7로 for 문도 함께 종료된다.

##