[Algorithm] 17. 부분합

N명의 시험 성적을 내림차순으로 정렬한 배열 scores[] 가 있다.

a등에서 b등까지 평균 점수를 계산하는 함수 average(a,b)를 만들어라.

scores[a] 부터 scores[b] 까지 순회하여 각 원소의 수를 더하고, b-a+1로 나누면 된다.

최적화할 수 없을까?

부분합(partial sum)

배열의 첫 번째 원소와 각 배열의 첫 번째 인덱스 부터 N까지의 합을 구해둔 배열임

부분 합 계산하기

vector<int> partialSum(const vector<int>& a) {
  vector<int> ret(a.size());
  ret[0] = a[0];
  for (int i = 1; i < a.size(); ++i) {
    ret[i] = ret[i-1] + a[i];
  }
  return ret;
}

int rangeSum(const vector<int>& psum, int a, int b) {
  if(a == 0) return psum[b];
  return psum[b] - psum[a-1]; 
}

부분 합으로 분산 계산하기

• 왼쪽 항 = sigma a 부터 b까지 A[i]^2
• 가운데 항 -2m(ab) + Sigma a 부터 b 까지 A[i]
• 오른쪽 항 = (b-a+1)m(a,b)^2

가운데 항, 오른쪽 항은 psum 으로 계산가능

왼쪽 항 = 제곱의 부분항을 미리 만들어두면 O(1)로 계산 가능

double variance(const vector<int>& sqpsum, const vector<int>& psum, int a, int b) {
  // 해당 구간의 평균을 계산
  double mean = rangeSum(psum, a, b) / doulbe(b - a + 1);
  double ret = rangeSum(sqpsum, a, b) - 2 * mean * rangeSum(psum, a ,b)
						    + (b - a + 1) * mean * mean;
  return ret / (b - a + 1);
}  

2차원으로의 확장

A[y1, x1] 에서 A[y2, x2] 까지의 직사각형 구간의 합을 계산해야 하는 경우, 2차원 부분 합 배열 필요

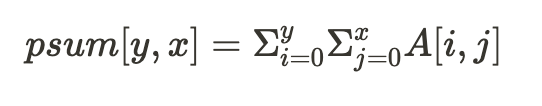
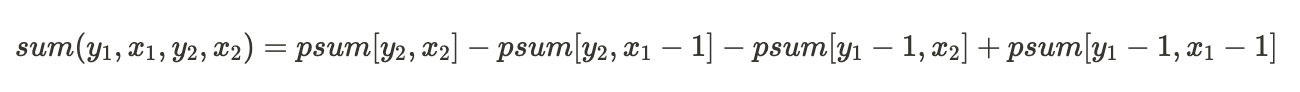
// psum[][] = 2차원의 배열 A[][] 의 부분 합
// A[y1, x1] 과 A[y2, x2] 양 끝을 갖는 부분 배열의 합 반환
int gridSum(const vector<vector<int>>& psum, int y1, int x1, int y2, int x2) {
  int ret = psum[y2][x2];
  if (y1 > 0) ret -= psum[y1-1][x2];
  if (x1 > 0) ret -= psum[y2][x1-1];
  if (y1 >0 && x1 >0) ret += psum[y1-1][x1-1];
  return ret;
}

예제: 합이 0에 가장 가까운 구간

합이 0에 가장 가까운 구간을 찾아라.

• A[] = 양수 음수가 모두 포함된 배열

i	0	1	2	3	4	5	6	7	8	9
A[i]	-14	7	2	3	-8	4	-6	8	9	11

정답은 A[2] ~ A[5] 까지가 0에 가장 가깝다(합은 1이다.)

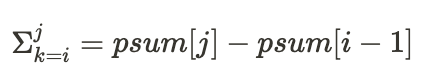
값이 0 에 가깝다는 것은 psum[j] 와 psum[i-1] 두 값의 차이가 가장 적다는 것과 동일한 의미다.

(단, j 는 i 보다 큰 인덱스여야 함)

// 원본 배열
[-14,  7,  2,  3,  -8,  4,  -6,  8, 9, 11]
// 부분합
[-14, -7, -5, -2, -10, -6, -12, -4, 5, 16]
// 부분합 정렬 
[-14, -12, -10, -7, -6, -5, -4, -2, 5, 16]
// 부분합 정렬 인덱스
[  0,   6,   4,  1,  5,  2,  7,  3,  8, 9]
// 인접한 원소끼리 뺀다
[  |2|, |2|,  |3|, |1|, |1|, |1|, |2|, |7|,|11|  ]
// 실제 배열 부분합
[1번~6번, 5번~6번, 2번~4번, 2번~5번 ...]

// 6번 부분합 - 0번 부분합 = -12 - -14 = 2
// 6번 부분합 = -14 -7 -5 -2 -10 -12
// 0번 부분합 = -14
// 6번 부분합 - 0번 부분합 = -7 -5 -2 -10 -12 = 1번~6번

[
PsumIndex{index=0, psum=-14}, 
PsumIndex{index=6, psum=-12}, 
PsumIndex{index=4, psum=-10}, 
PsumIndex{index=1, psum=-7}, 
PsumIndex{index=5, psum=-6}, 
PsumIndex{index=2, psum=-5}, 
PsumIndex{index=7, psum=-4}, 
PsumIndex{index=3, psum=-2}, 
PsumIndex{index=8, psum=5}, 
PsumIndex{index=9, psum=16}
]

• 부분합 정렬 후 인접한 원소에서 뺄 때, 인덱스가 큰 부분에서 작은 부분을 빼야 한다?
  • 만약, 0번 부분합에서 6번 부분합을 빼면 ( [-14] - [-14, -7, -5, -2, -10, -12] )
  • 6번 부분합에서 0번 부분합을 뺀 합이 음수가 되어버림( [7, 5, 2, 10, 12] )
    • 7+5+2+10+12=36
  • 하지만, 구간의 합이 0에 가까운 값을 찾는 것이므로 절대값을 해주면 결과는 같음