[Algorithm] 22 이진 검색 트리 - 3
노드 삭제와 ‘합치기’ 연산
기존 이진 검색 트리에서의 노드 삭제와 별반 다를 게 없다.
두 서브트리를 합칠 때 어느 쪽이 루트가 되어야 하는지를 우선순위를 통해 판단하는 점만 제외하면 거의 똑같다.
기존 이진 검색 트리에서의 삭제를 구현하는 방법은 여러가지 있지만,
그중 합치기 연산으로 구현하는 것이 간편하다.
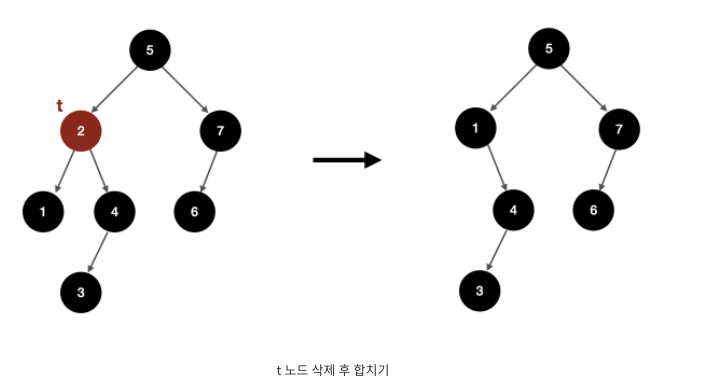
노드 t를 지울 거라면, t의 두 서브트리를 합친 새로운 트리를 만든 뒤
이 트리를 t를 루트로 하는 서브트리와 바꿔치기한다.
트립의 루트는 우선순위로 결정되기 때문에, A의 최대 우선순위와 B의 최대 우선순위를 비교해줘야 한다.
- a(1)의 우선순위가 b(4)의 우선순위보다 더 크다면 a(1)의 오른쪽 자식으로 a(1)의 오른쪽 서브트리와 b(4)를 합쳐서 붙인다. a.setRight(merge(a.right, b));
- 반대로 b의 우선순위가 더 크다면 b의 왼쪽 자식으로 a와 b의 왼쪽 자식을 합쳐서 붙인다. b.setLeft(merge(a,
- b.left));
구현
// root를 루트로 하는 트립에서 key를 지우고 결과 트립의 루트를 반환한다.
public Node erase(Node root, int key){
if(root == null) return root;
// root를 지우고 양 서브트리를 합친 뒤 반환한다.
if(root.key == key){
Node ret = merge(root.left, root.right);
root = null;
return ret;
}
if(root.key > key){
root.setLeft(erase(root.left, key));
} else{
root.setRight(erase(root.right, key));
}
return root;
}
// a와 b가 두 개의 트립이고, max(a) < min(b)일 때 이 둘을 합친다.
private Node merge(Node a, Node b){
if(a == null) return b;
if(b == null) return a;
if(a.priority < b.priority){
b.setLeft(merge(a, b.left));
return b;
}
a.setRight(merge(a.right, b));
return a;
}
K번째 원소 찾기
그와 같은 기능 중 하나가 주어진 서브트리의 노드들을 포함한 원소의 크기 순으로 나열했을 때
k번째로 오는 노드를 찾는 연산이다.
Node 클래스에서 서브트리의 크기 size를 계산해 저장해 두기 때문에 이것을 구현하기란 어렵지 않다.
root를 루트로 하는 서브트리는 왼쪽 자식 root → left를 루트로 하는 서브트리와
오른쪽 자식 root → right를 루트로 하는 서브트리 그리고 root 자신으로 구성되어 있다.
각 서브트리의 크기를 알고 있으면 k번째 노드가 어디에 속해 있을지 쉽게 알 수 있다.
왼쪽 서브트리의 크기를 l이라 할 때, 다음과 같이 세 가지의 경우로 나눌 수 있다.
- k ≤ l : k번째 노드는 왼쪽 서브트리에 속해 있다.
- k = l+1 : 루트가 k번째 노드이다.
- k > l+1 : k번째 노드는 오른쪽 서브트리에서 k-l-1번째 노드가 된다.
// root를 루트로 하는 트리 중에서 k번째 원소를 반환한다.
public Node kth(Node root, int k) {
// 왼쪽 서브트리의 크기를 우선 계산한다.
int leftSize = 0;
if (root.left != null) {
leftSize = root.left.size;
}
if (k <= leftSize){
return kth(root.left, k);
}
if (k == leftSize + 1)
return root;
}
return kth(root.right, k - leftSize - 1);
}
 | root | k | kth(root, k) | k ≤ l | k == leftSize + 1 | kth(root→right, k - leftSize -1) |
| — | — | — | — | — | — |
| 5 | 4 | kth(5, 4) | 4 ≤ 4 True | | |
| | | kth(2, 4) | 4 ≤ 1 False | | kth(4, 4-1-1)
kth(4, 2) |
| | | kth(4, 2) | 2 ≤ 1 False | 2 == 1 + 1
return 4 | |
| root | k | kth(root, k) | k ≤ l | k == leftSize + 1 | kth(root→right, k - leftSize -1) |
| — | — | — | — | — | — |
| 5 | 4 | kth(5, 4) | 4 ≤ 4 True | | |
| | | kth(2, 4) | 4 ≤ 1 False | | kth(4, 4-1-1)
kth(4, 2) |
| | | kth(4, 2) | 2 ≤ 1 False | 2 == 1 + 1
return 4 | |
**X보다 작은 원소 세기**
특정 범위 [a, b]가 주어질 때 이 범위 안에 들어가는 원소들의 숫자를 계산하는 연산이 있다.
이 연산은 주어진 원소 X보다 작은 원소의 수를 반환하는 countLessThan(x)로 가능하다.
- [a, b] 범위 안에 들어가는 원소들의 수는 countLessThan(b) - countLessThan(a)로 표현
countLessThan(x)는 탐색 함수를 변형해 간단하게 만들 수 있다.
- 먼저 root의 원소가 x보다 큰지 비교한다.
- 만약 root의 원소가 x보다 같거나 크면 root와 오른쪽 서브트리에 있는 원소들은 모두 x이상이므로, 왼쪽 서브트리에 있는 원소들만 재귀적으로 세서 반환하면 된다.
- 만약 root의 원소가 x보다 작다면,
- 그 왼쪽 서브트리에 있는 원소들을 모두 x보다 작으므로 재귀적으로 세지 않아도 전부 답에 들어간다는 것을 알 수 있다.
- 오른쪽 서브트리에서 x보다 작은 원소를 재귀적으로 찾고 이것에 왼쪽 서브트리에 포함돈 노드 및 루트의 개수를 더해주면 된다.
// X보다 작은 키를 갖는 노드의 수를 반환
public int countLessThan(Node root, int x) {
if (root == null) {
return 0;
}
if (root.key >= x) {
return countLessThan(root.left, x);
}
// x가 현재 노드보다 클 경우
// 왼쪽 서브트리 크기 + 현재 노드 + 오른쪽에서 x보다 작은 노드 수
int ls = root.left == null ? 0 : root.left.size;
return ls + 1 + countLessThan(root.right, x);
}
우선순위 큐와 힙
- 우선순위 큐는 일반 큐와는 달리 우선순위가 가장 높은 자료가 가장 먼저 꺼내지는 자료구조
- 수행할 작업이 여러 개 있고 시간이 제한되어 있을 때 우선순위가 높은 것부터 수행하는 경우 사용
우선순위 큐를 구현하는 방법
- 연결리스트, 배열
- 료구조에 원소를 모두 집어넣고, 원소를 꺼낼 때 마다 모든 원소를 순회하며 우선순위가 높은 원소를 찾는 방식을 사용해야 하는데, 이러면 원소 추가 O(1), 검색 O(n)이 걸린다.
- 균형잡힌 이진 검색 트리
- 구현이 어렵다.
- 원소들을 우선순위로 정렬해 두면 최대 원소 삭제와 원소 삽입 모두 O(logN) 시간에 할 수 있다.
- 힙
- 호율적인 방법은 바로 힙(Heap)으로 구현하는 것
- 이진 검색 트리보다 훨씬 간단한 구조로 구현할 수 있다
- 최적화된 형태의 이진 트리로, 힙을 사용하면 원소를 추가하는 연산과 가장 큰 원소를 꺼내는 연산 모두 O(logN) 시간에 할 수 있다.

힙 구현
힙의 모양 규칙에 의해, n개의 노드가 있을 때
이 노드들은 arr[0]에서 arr[n-1]까지 순차적으로 대응된다.
- arr[i]의 왼쪽 자식은 arr[2*i + 1]에 대응된다.
- arr[i]의 오른쪽 자식은 arr[2*i]에 대응된다.
- arr[i]의 부모는 arr[(i-1)/2]에 대응된다. (나눗셈 결과는 내림한다.)
