[Algorithm] 22 이진 검색 트리 - 2

트립의 구현

필드에는 key, priority를 가진다. 노드가 생성될 때 랜덤 함수로 우선순위를 부여한다.

또 하나 유의할 점은 자신을 루트로 하는 서브 트리에 포함된 노드의 수를 저장하는 size 멤버이다.

• 이 값은 left, right가 바뀔 때마다 자동으로 갱신되며, 이 값을 이용하면 k번째 원소를 찾는 연산이나 X보다 작은 원소를 세는 연산 등을 쉽게 구현할 수 있다.

class Node {
	int key; // 노드에 저장된 원소
	int priority; // 이 노드의 우선순위(proirity)
	int size; // 이 노드를 루트로 하는 서브 트리의 크기
	
	Node left, right;

	// 초기화 및 난수 우선순위 생성
	Node(int key) {
		this.key = key;
		this.priority = new Random().nextInt(100);
		this.left = this.right = null;
	}

	void setLeft(Node left) {
		this.left = left;
		calcSize();
	}

	void setRight(Node right) {
		this.right = right;
		calcSize();
	}

	void calcSize() {
		size = 1;
		if (left != null) {
			size += left.size;
		}
		if (right != null) {
			size += right.size;
		}
	}
}

특징

• 트립의 노드 객체는 포함하는 원소 key 외에도 우선 순위를 가짐
• 자신을 루트로 하는 서브트리에 포함된 노드의 수를 저장하는 size 멤버 함수 존재
• 이 값은 left, right가 바뀔 때마다 자동으로 갱신
• 이 값을 이용하면 k번째 원소를 찾는 연산이나 x보다 작은 원소를 세는 연산 등을 쉽게 구할 수 있음

노드 추가와 ‘쪼개기’ 연산

root를 루트로 하는 트립에 새 노드 node를 삽입해보자.

가장 먼저 확인해야 할 것은 root와 node의 우선순위다.

root 우선순위 > node 우선순위

만약 root의 우선순위가 더- 높다면 node는 root 아래로 들어가야 한다.

left, right는 두 노드의 원소를 비교해서 정하고, 재귀를 통해 삽입한다.

root 우선순위 < node 우선순위

문제가 되는 것은 node의 우선순위가 root보다 높은 경우이다.

이때는 node가 기존에 있던 루트 root를 밀어내고 이 트리의 포함되어 있던 노드들은 모두 node의 자손이 되어야만 한다.

이것을 구현하는 좋은 방법은 기존의 트리를 node가 가진 원소를 기준으로 ‘쪼개는’ 것이다.

구현 방법

트리를 쪼개서 기준보다 작은 원소만을 갖는 서브트리 하나, 큰 원소만을 갖는 서브트리로 두면 삽입 작업은 완료된다.

root를 루트로 하는 서브트리를 원소가 key보다 작은 노드들과 큰 노드들로 쪼개는 split(root, key)를 작성해보자.

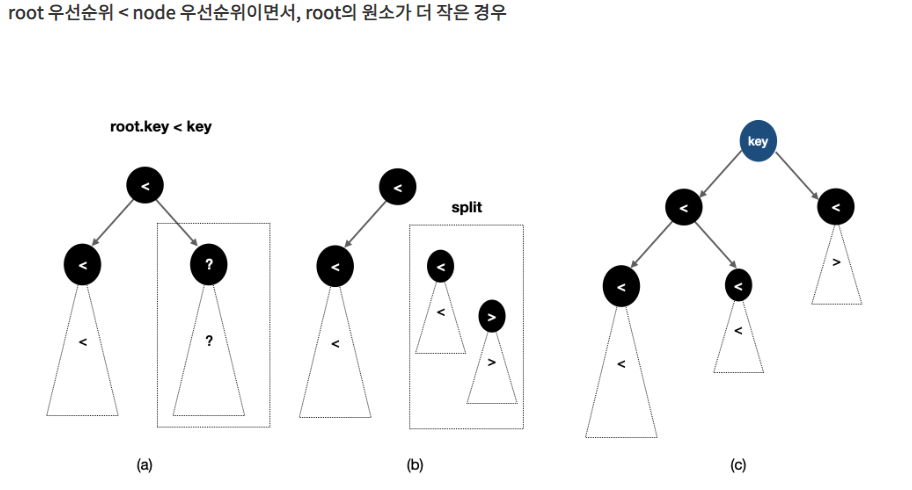
root의 원소가 key보다 작기 때문에 그 왼쪽 서브트리의 원소들은 전부 key보다 작을 수밖에 없다. **

따라서 key보다 큰 원소가 있을 수 있는 곳은 점선으로 표현된 오른쪽 서브트리 뿐이다.

1. 재귀 호출을 적용해 (b)처럼 해당 트리를 key를 기준으로 쪼갠다.
2. 쪼갠 결과 중 key보다 작은 원소를 갖는 트리를 root의 오른쪽 자손으로 연결한다.

3. 그러면 key보다 작은 원소를 갖는 트리와 key보다 큰 원소를 갖는 트리가 남게되는데,

   이 두 개의 트리가 각각의 key를 루트로 하는 왼쪽 서브트리와 오른쪽 서브트리가 되는 것이다.

구현

public class Treap {
	public Node insert(Node root, Node node){
		if(root == null){
			return node;
		}

		//추가하려는 노드가 루트보다 크면
		if(root.priority < node.priority){

			Node[] splitted = split(root, node.key);
			node.setLeft(splitted[0]);
			node.setRight(splitted[1]);
			return node;

		}else if(root.key > node.key){
			root.setLeft(insert(root.left, node));
		}else {
			root.setRight(insert(root.right, node));
		}
		return root;
	}

	public Node[] split(Node root, int key) {
		Node[] pair = new Node[2];
		if (root == null) {
			return pair;
		}
        
  	// 루트가 key 미만이면 오른쪽 서브트리를 쪼갠다.
		if (root.key < key) {
			Node[] rs = split(root.right, key);
			root.setRight(rs[0]);
			return new Node[]{root, rs[1]};
		} else { // root가 key 이상이면 왼쪽 서브트리를 쪼갠다.
			Node[] ls = split(root.left, key);
			root.setLeft(ls[1]);
			return new Node[]{ls[0], root};
		}
	}
}