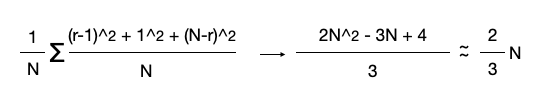[Algorithm] 22 이진 검색 트리
22.3절 이진 검색 트리에서의 문제점
- 특정 형태의 입력에 대해 연결 리스트가 되어버리는 문제
- 균형 잡힌 이진 검색 트리는 구현이 어려움
결론:
그래서 경험있는 프로그래밍 대회 참가자들은 구현이 간단한 이진 검색 트리를 사용하고
대표적인 예: 트립
트립
- 랜덤화된 이진 검색 트리
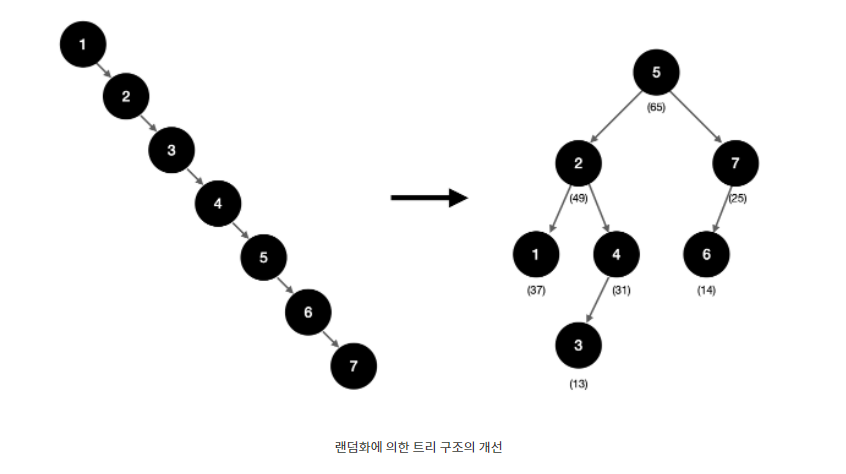
- 트리의 형태가 원소들의 추가 순서에 따라 결정되지 않고 난수에 의해 임의로 결정
- 원소들이 어느 순서대로 추가되고 삭제되더라도 트리 높이의 기대치는 항상 일정
- 이와 같은 속성을 유지하기 위해 트립은 새 노드가 추가될 때마다 해당 노드에 우선 순위를 부여
- 이 우선 순위는 원소의 대소 관소관계나 입력 순서에 상관없이 난수를 통해 생성
- 트립은 항상 부모의 우선 순위가 자식의 우선 순위보다 높은 이진 검색 트리를 만듭니다.
트립의 두 가지 조건
트립은 항상 부모의 우선순위가 자식의 우선순위보다 높은 이진 검색 트리를 만든다
따라서 트립의 조건을 다음 두 가지로 정의할 수 있다.
- 이진 검색 트리의 조건
- 모든 노드에 대해 왼쪽 서브트리에 있는 노드들의 원소는 해당 노드의 원소보다 작고,
오른쪽 서브트리에 있는 노드들의 원소는 해당 노드의 원소보다 크다.
- 힙의 조건
- 모든 노드의 우선순위는 각자의 자식 노드보다 크거나 같다.
트립의 높이
이와 같은 랜덤화가 의미가 있으려면 노드의 순서를 임의로 바꿨을 때 트리 높이의 기대치가 O(N)보다 작아야 한다. 그렇지 않으면 제약을 추가한 의미가 없다.
N개의 원소를 갖는 트립에서 어떤 원소 x를 찾으려 한다. 이때 방문해야 하는 노드 수의 기대치가 O(logN)임을 증명해보자.
“이것을 증명하는 한 가지 방법은 트리를 한 단계 내려갈 때마다 후보가 되는 원소의 수가 선형으로 줄어드는 것이 아니라 지수적으로 줄어드는 점을 보이는 것이다.”
트립의 루트는 N개의 노드 중 최대 우선순위를 가진다. 루트가 갖는 원소가 N개의 원소 중에서 r(r≥1)번째로 작은 원소라고 하자. 그러면 왼쪽 서브트리에는 r-1개, 오른쪽 서브트리에는 N-r개의 노드가 있을 것이다.
각 원소가 우리가 원하는 원소일 확률이 모두 동등하다고 가정하면,
- 우리가 찾는 원소가 왼쪽 서브트리에 있을 확률은 (r-1)/N,
- 루트에 있을 확률은 1/N,
- 오른쪽 서브트리에 있을 확률은 (N-r)/N 이 된다.
따라서 다음 단계에서 후보의 수의 기대치는 다음과 같다.
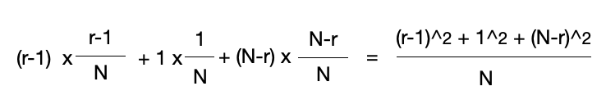
우선순위를 임의로 부여하기 때문에 모든 값은 루트가 될 가능성이 같다.
따라서 모든 r에 대한 값의 평균을 구해보면 대략 2N/3이 나오게 된다.
다시 말해 한 단계 내려갈 때마다 후보의 수가 평균적으로 2/3으로 줄어든다는 뜻이다.
따라서 O(logN) 단계를 거치면 답을 찾을 수 있음을 알 수 있다.
증명
- 트리가 한 단계 내려갈 때마다 존재할 수 있는 노드의 수가 지수적으로 줄어든다.
- 만약 N = 90이고 루트의 층이 1층이라면, 2층에서의 후보는 60가 되고 3층에서의 후보는 40 … 로 줄어든다. 따라서 (2/3)^h*N으로 계속해서 줄어들게 된다.